Quantitative Survey Data Collection
Defining the Population
A sample in a market research study is drawn from a population (sometimes called a universe). For example, when conducting political polls, our population is the people who can vote in the next election. When conducting studies of fast moving consumer goods (e.g., breakfast cereal or laundry detergent), our population is grocery buyers.
The unit
Defining the population for a study involves two separate decisions. The first decision is what unit to study. The unit is the ‘what’ that is to be counted. Commonly-used units include people, consumers, users, households, main grocery buyers, businesses, business decision makers and voters.
The boundaries
The second decision is to define the boundaries of the population: which units are included and which are excluded. Most obviously this is done via geography, where a decision is made about which countries (or states within countries) should be included in the research. Typically boundaries are also defined based on behavior, such as consumption of a particular product. Examples of population definitions for studies include:
- Main Grocery Buyers who have purchased instant coffee in the past four weeks in Australia.
- People who will be eligible to vote in the next US Presidential Election.
The classic mistake
A common mistake when defining population is to over-define the population such that it is too small. One chip manufacturer undertook a study where the market was defined as “Males aged 25 to 34 who have consumed premium chips in the past two weeks”. When it was suggested that the market was too narrow to be sensible, the brand manager indicated that this was not a problem as the age group was “aspirational”. The reason that such a narrowly defined market is problematic is that inevitably most of the people who are really in the market for the product are not represented by the study and thus the study likely becomes biased.
There are some simple rules of thumb that can be used to see if a population has been too narrowly defined:
- If the biggest selling products in the market are getting more than 20% of their sales from people outside the defined market, the definition is likely too narrow.
- If the definition involves any demographic variables (e.g., age, gender, income), it is probably a Target Market rather than a sensible population definition. The exception is if the demographics are causally related to aspects of people’s physiology or life circumstances. For example, if the study is about retirement, then age is causally related to this, whereas if the study is about chip buying, age may be correlated but is not causally related.
- The definition must be operational. For example, rather than “women capable of bearing children” a more operational definition is “women aged 12 to 50”.
Selecting a Sample
Once the population has been defined, we need a way of finding the people in the population. To do this we need either a list of people in the population, or, a list of places where we can find people.[note 1]
Surveys involve either selecting everybody from a list or at a specific location (which is known as a census), or sampling, which involves randomly selecting people from lists or locations.
Lists
Common examples of lists include:
- Online panels, which are databases of people willing to participate in market research in return for pay or prizes.
- Telephone directories.
- Delivery Point IDs, which are lists of all the postal addresses in Australia.
- Lists of customers’ email addresses.
- Lists of people willing to participate in focus groups and depth interviews (these lists are held by recruiters).
Such lists are sometimes referred to as the sample. However, it is important not to confuse this with use of the word sample with its normal meaning (respondents that have completed the questionnaire).
Places
Common examples of lists of places where we can find people include:
- Shopping centres.
- Websites’ banner advertisements (e.g., “click here to earn money”).
- List of telephone prefixes (which can be used to randomly generate phone numbers).
- Suburbs, where face-to-face interviews may knock on, say, every fifth door.
- People who phone in to phone-in-polls run by TV stations.
Checking to see if the list is good
The coverage of a survey refers to the extent to which people in the population (e.g., consumers in the market) could potentially have been included in the study. A challenging aspect of all surveys is that most people are unwilling to participate. This means that all surveys tend to have poor coverage. For example, most surveys are conducted using online panels and around 1% of the population is on these panels.
Coverage error is error that occurs when the list is not representative of the population in terms of the things being measured. Consider, for example, using an online panel to understand attitudes to the internet. People who do not use the internet will not be on such a panel and, consequently, any online study seeking to understand attitudes to the internet in the general community will be massively biased.
In an ideal world for research, we would have access to lists containing everybody in the population. This rarely happens in practice. Even companies’ lists of their customers are generally incomplete, due to people having provided incorrect contact details, having changed contact details or having advised the company they do not want to participate in market research. Consequently, when evaluating whether coverage error is a problem for a survey, our focus is not on working out whether the list contains 100% of the population. Rather, our focus is on determining whether the factors that cause somebody to be omitted from a list will be correlated with how the data they would have provided if they had been included. For example, it is problematic to use the telephone directory as a list if conducting a study of high net worth individuals, as wealthier people are more likely to have unlisted numbers.
Selecting from the list
Often you will not want to attempt to interview everybody on your list. Typically, if you have a large list, the process is:
- Work out your required sample size.
- Take a guess at your response rate, which is the proportion of people that complete an interview relative to the proportion that you invite to the interview. For example, if you invite 10,000 people and 1,000 complete the interview then you have a 10% response rate. It is best to be pessimistic when guessing your response rate.
- Select the required number of people from your list. E.g., if you need 1,000 interviews and your response rate is 10% then you need to select 10,000 people from the list. The process of selecting these people from the list should be random. A simple way to achieve this outcome is to take, say, every 20th person from your list (or a different number based on the size of the list).
Deciding How to Conduct the Interviews
The vast majority of quantitative market research surveys are conducted online. Nevertheless, there are many other ways of data collection, including in-store interviews, phone interviews, online qual, SMS interviews, door-to-door interviews and mail interviews.
There are numerous different considerations that need to be traded off when choosing how to collect data, including cost, time taken to conduct the research, the ability to show stimulus (e.g., videos, images). In the main, these trade-offs are straightforward to make. The only difficult issue in most real-world surveys relates to coverage.
Coverage
Different ways of conducting interviews ‘cover’ different proportions of the population. For example, if you work out how the market works by asking your best friend, you have only covered a minuscule proportion of the market. The proportion of the market that can potentially be included in your survey is its coverage. For example, if you decided to conduct a survey by phoning 200 people on a Wednesday evening, the coverage will consist of all the people who:
- Were at home at the times that you could have called them.
- Will have answered the phone.
- Were in the list of phone numbers that you selected your sample from.
Note that the idea of coverage relates to people that you could potentially have contacted, as opposed to those that you did contact.
Minimizing coverage error
It is good practice to choose to collect data in the way that will reduce coverage error. For example, many service companies still conduct important market research by phone, even though it costs more than ten times as much per interview as an online interview. They do this because they often have their customers’ phone numbers but are less likely to have all of their customers email addresses. In other words, the list of email addresses has worse coverage than the list of phone numbers.
Coverage error is an endemic problem in market research. As a general rule, the cheapest forms of data collection suffer from the worst sample selection biases. Consider the phone in polls used by TV stations and the web polls run by online newspapers.
Example
Consider a chain of gyms wanting to understand how to increase gym attendance. It seems evident that the people that have the most active lifestyles will be spending less time using computers and are thus less likely to participate in online surveys, meaning that if an online survey is conducted it will over-represent unfit people and thus using an online survey will result in coverage error.
While it is clear that conducting an online survey is far from the ideal way of conducting a survey of looking at the exercise market, all of the other options suffer from similar problems and some, such as phone and door-to-door interviewing are considerably more expensive, and thus, unless hundreds of thousands of dollars are available for the survey, conducting such a survey online is usually the only practical solution. Importantly, this does not make the online sample ‘valid’. Rather, it simply makes it the tallest dwarf. We need to keep this in mind when interpreting the data from such a survey (and from most online surveys for that matter).
Determining The Sample Size
Precision and sample size
Consider a simple survey question such as:
How likely would you be to recommend Microsoft to a friend or colleague? Not at all Extremely likely likely 0 1 2 3 4 5 6 7 8 9 10
This question was asked of a sample of 312 consumers and the following frequency table summarizes the resulting data:
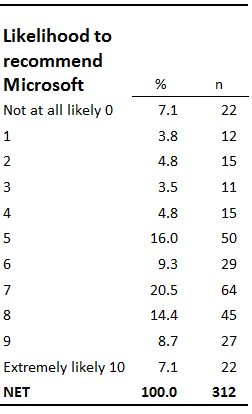
From this table, we can compute that the average rating given to Microsoft is (0×22+1×12+…+10×22)/312=5.9 out of 10. However, only 312 people have provided data. As there are around seven billion people in the world, it is possible that we would have computed a different answer had we interviewed all of them. But how different? This is the question we seek to understand by evaluating precision.
The most common way of communicating the precision of an estimate to a non-technical audience is using confidence intervals. If we use the simplest formula for computing confidence intervals, we compute that the 95% confidence interval for likelihood to recommend Microsoft is from 5.6 to 6.2, which can be interpreted loosely as the range in likely true values that would have been obtained had everybody been interviewed (i.e., based on the survey, we would be surprised if the true figure, obtained by interviewing everybody in the world, was not in the range of 5.6 to 6.2).
Formulas for computing confidence interval take the sample size as an input. With a total of 312 respondents in the sample the confidence interval is 5.6 to 6.2. With a larger sample size there is a smaller confidence interval. Similarly, with a smaller sample size a bigger confidence interval is computed. For example, if we halve, double or quadruple the sample size (n) we can compute the resulting 95% confidence intervals shown in the table below (if this table was not rounded to the first decimal place a more gradual change in the confidence intervals for different sample sizes would be evident).
| n | Lower bound | Upper bound | Interval |
|---|---|---|---|
| 156 | 5.4 | 6.3 | 5.87±0.43 |
| 312 | 5.6 | 6.2 | 5.87±0.31 |
| 624 | 5.6 | 6.1 | 5.87±0.22 |
| 1,248 | 5.7 | 6.0 | 5.87±0.15 |
The right-hand side of the table shows the confidence interval in a slightly different way, represented as the mean with a figure ±. If you have ever read a political poll you will have seen this before, where it is described as the margin of error (e.g., a political poll may report a result of 50% with a margin of error of 3%).
A key thing to note about the confidence intervals is that although they get smaller with larger sample sizes, there are diminishing returns. In the example, the largest sample size of 1,248 is 8 times as big as n = 156, but the resulting confidence interval for n = 156 is less than three times as big as that for 1,248.
Guidelines for determining sample size
A practical challenge when designing a study is working out how large a sample is required. Although larger sample sizes reduce the sampling error – that is, the width of the confidence intervals – larger sample sizes cost more money. From time-to-time it is possible to work out the required sample size by working backwards from a desired confidence interval. For example, if Microsoft indicated they wanted to measure the average likelihood of being recommended to within ±0.22, we could determine that this required a sample size of 624. In practice, it is extraordinarily unusual rare for such computations to be used to determine sample size. Instead, market researchers use a combination of gut feel, rules of thumb and understanding of their clients’ need for accuracy when working out sample sizes. Some rough rules of thumb for sample size in quantitative studies are: n = (Total budget – fixed costs)/cost per interview n ≥ 300 for basic studies n ≥ 600 for segmentation studies n ≥ 1000 for important strategic studies n ≥ 100 per subgroup (e.g., segment)
Sample sizes with small populations
It is intuitively obvious to most people that if sampling from a small population then you can use a smaller sample size. This intuition is wrong. Unless the sample size is going to be 20% or more of the size of the population, it actual size of the population is pretty-much irrelevant in terms of determining confidence interval and thus is not a factor in working out the required sample size.
That is, the estimated confidence interval of 5.6 to 6.2 is the same width regardless of whether the study had been conducted in a population of 10,000 or 10 billion people. This is mostly good news. It means that there is virtually never a need for super-large samples (e.g., 10,000 or more). Even in China, the sample size used to measure the TV ratings is 14,650,[1] and the reason it is so large is not because the population is so large, but because there is a need to divide the country up into regions and have relatively narrow confidence intervals within the regions. A flipside of this is that in Australia sampling market research is comparatively expensive, because even though the population is relatively small, the sample sizes still need to be broadly equivalent to those in much larger countries (the Australian TV ratings sample is about one-third the size of the Chinese sample, even though the Chinese population is more than 50 times larger).
Nevertheless, when sampling from relatively ‘small’ populations (e.g., in business-to-business studies), it is commonplace to use a smaller sample size than in a survey of consumers. However, this is principally because the cost-per-interview is substantially greater in business-to-business surveys.
Setting Quotas
Most surveys employ quotas, sometimes referred to as strata or stratification, to ensure that the data is representative on key variables.
Example
A study of 2,000 energy households used the following quotas. The key logic behind the quotas in this example is that the structure of a household is a key determinant of its energy usage patterns and levels and thus ensuring that the sample is consistent with these quotas provides some assurance that the survey will accurately capture the true variation between households in terms of their energy usage.
| Quota Group | Quota | Proportion |
|---|---|---|
| Couple – youngest child aged 11 or under | 466 | 23% |
| Couple – youngest child aged 12 to 17 | 186 | 9% |
| Couple – children at home aged 18 or more | 128 | 6% |
| One parent family – youngest child aged 11 or under | 120 | 6% |
| One parent family – youngest child aged 12 to 17 | 56 | 3% |
| One parent family – children at home aged 18 or more | 46 | 2% |
| No Children – 18 to 24 | 140 | 7% |
| No Children – 25 – 34 | 238 | 12% |
| No Children – 35 – 44 | 158 | 8% |
| No Children – 45 – 54 | 208 | 10% |
| No children – 55 or more | 254 | 13% |
| Total | 2,000 | 100% |
Interlocking and non-interlocking quotas
The quotas shown above involve multiple variables: household structure and age. Such quotas are referred to as interlocking quotas. An alternative approach is to have separate quotas by each variable, non-interlocking quotas, for example:
| Quota group | Quota |
|---|---|
| Mainly use PC | 100 |
| Mainly use Macintosh | 100 |
| Aged under 30 | 66 |
| Aged 30 to 50 | 67 |
| Aged more than 50 | 67 |
If using these quotas and randomly selecting respondents from an online panel, there is a good chance that by the time 150 interviews have been conducted, the PC quota will be filled (because many more people in the population use PCs so the quota will fill faster) and the two younger quotas will be filled (because most people in online panels are younger). Thus, these quotas may result in the last 50 respondents being Mac users aged more than 50. The resulting data will seem to reveal a strong correlation between age and Mac usage, whereas the reality is that the correlation has been created by the use of overlapping quotas.
A natural conclusion to reach from this example is that we should have large tables of interlocking quotas. For example, hundreds of quota groups defined by age, gender, household structure, geography, and any other key variables. Unfortunately, this is impractical. We generally do not have data to permit us to work out how many customers we have aged 18 to 24 living in NSW in a group household with no children, which makes it impossible to create good quotas. Further, even if we could create the quotas, large numbers of quotas are very expensive, as there always ends up being a few quota groups that are extraordinarily hard to fill.
Proportional versus non-proportional quotas
Most quotas are proportional, which is to say that the number of respondents required in each group is determined by the number of people in the population believed to be in each group (e.g., based on ABS published statistics). Sometimes the quotas may be non-proportional to ensure enough people in a key segment are in the study (e.g., if doing a study for Apple, you may want 50% of the sample to be Apple customers); if employing non-proportional quotas the data needs to be weighted and this requires that you know the correct population proportions for weighting.
Online interviewing and send quotas
Developing quotas for online interviewing requires an additional step to that described above. In addition to creating quotas relating to how many people complete the survey (which is what the above descriptions relate to) there is additionally also a need to create quotas relating to the number of people invited to participate. These should always be interlocking and it is generally advisable to create a large number of quotas (e.g., creating quota categories of 5 year age bands by gender by geography).
Some online panel companies refer to such quotas as weighting.
A good quality online study requires both quotas of the sends and quotas on the number of completes. Where quotas are only provided on the number of completes it can lead to bizarre results. For example, in one study which used the age bands of Under 30, 30 to 50 and 51 or more, almost all of the respondents in the 51 or more category were 51 years old, meaning that the survey had no representation of older consumers. When quotas are used on the sends but not on the completes, the result tends to be an over-representation of older consumers, because they are more likely to respond to an invitation to participate.
Code Frame
The list of Values and their associated interpretations in a question. For example, in a question asking about gender, the code frame is:
| Value | Value Label |
|---|---|
| 1 | Male |
| 2 | Female |
The specific terms of Value and Value Label are the terms used most commonly (e.g., in SPSS, Q and Displayr). However, there is no standard terminology (e.g., some researchers refer to the Value Label as a ‘code’ and others refer to the Value as a ‘code’.
The code frame will typically be created in one of the following ways:
- It will exist in the questionnaire.
- When the questionnaire is programmed the categories will be entered (i.e., the Value Labels) and the Values will automatically be generated by the program (typically, with a 1 for the first category of a single response question, a 2 for the second category, etc.).
- It will be created at the time of coding the text data.
- It will be created using the first two methods and then modified during the coding of Other (specify) options.
Multiple response questions
The meaning of the code frame in a multiple response question is slightly ambiguous. Most commonly, it will refer to the list of options and there will not be any specific values assigned to each of these values. However, the ambiguity is that the variables that constitute a multiple response question will typically have their own code frame, which will usually be something like:
| Value | Value Label |
|---|---|
| 0 | Not selected |
| 1 | Selected |
or
| Value | Value Label |
|---|---|
| 1 | Yes |
| 2 | No |
Fielding the Survey
Fielding is the industry jargon for conducting the actual survey.
The soft send
In online surveys it is good practice to conduct a soft send once the survey has been programmed and tested. This involves sending enough invitations such that, say, 50 to 100 interviews, are completed. The resulting data is then used to test and check various assumptions about the research design. In particular:
- Does the resulting sample appear to be sensible (see Checking Representativeness).
- How much effort will it take to achieve the desired number of interviews (e.g., how many people will be invited to participate).
- Will it be possible to achieve the desired number of interviews.
- Is the resulting data sensible and useful. Generally this can only be assessed by creating and reviewing a summary report.
Checking quotas and sample size
Additional interviews are conducted until the sample size and the specified quotas have been achieved. Where there is a particular problem filling some of the quotas this means that either there is a problem with the list being used, or, that the quotas are wrong. Either way, it is important to carefully review any difficulties in achieving quotas rather than to continue to collect data until the quotas are all filled as a difficulty in filling a quota can indicate that the resulting sample has a coverage bias.
Programming and Testing
Programming refers to entering the questionnaire into the Data Collection Software and testing refers to checking that it has been programmed correctly. Key things to check are that:
- The skips in the questionnaire make sense. That is, that there are no combinations of options that people select which cause them to receive an error message or to be shown the wrong questions.
- That anybody can do the questionnaire. One old or very young family member is one good way of checking.
- That the data exports correctly. This is done by creating and reviewing a Summary Report.
It is good practice to conduct a pilot survey to a dozen respondents and check that the resulting data is as anticipated. An even better practice is to sit with these respondents as they are doing the survey and ask them to think aloud, explaining how and why they are answering the questions, as this can given insight into any problems with question wording.
Data Collection Software
Comparison table of services
The table below presents some of the services that offer online survey creation and deployment. For analysis, the most important factor is the availability of an appropriate data file. SPSS data files are usually the best of the file types available in the cheaper data collection programs as they contain metadata that allows software to interpret the meaning of the data. CSV and other spreadsheet formats require more work to set up data in analysis software packages. Companies marked with an “N/A” for data files either:
- Don’t supply SPSS data files
- Did not have data files available to inspect for quality
If you wish to suggest improvements/changes to the table below please provide some detail and a contact email in the comment form at the bottom of this page.
| Company | Cheapest Package | Cheapest package with complete data export | Interesting Features |
|---|---|---|---|
| SurveyMonkey | Basic – Free | Gold – $300/year
|
|
| Alchemer (formerly Survey Gizmo) | SG Lite – Free | Alchemer (formerly Survey Gizmo) – $810/year
|
|
| QuestionPro | Free | Corporate – $1008/year
|
|
| Qualtrics | Free account | Research Suite – N/A
|
|
| Snap Surveys | N/A | Single PC Installation with hosting – $1,995 + $395/year
|
|
| Toluna QuickSurveys | Free | NA |
|
| Super Simple Survey | The Basic – Free | NA |
|
| Polldaddy | Free | N/A |
|
| Obsurvey | Free | N/A |
|
| Wufoo | Free | N/A |
|
| Insightify | Free | N/A | |
| Survey Crafter | $495 for a single license | N/A |
|


