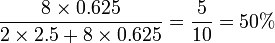Data Preparation
Cleaning, tidying, and weighting are activities that are performed before trying to work out what the data in a survey means.
- Data cleaning refers to checking and correcting anomalies in a data file. The goal is to identify data that is, in some way, clearly incorrect. The unglamorous world of data cleaning can be a key determinant of the quality of data analysis, particularly when the data is from a messy source (e.g., customer records, collected using a cheap data collection program).
- Data tidying involves manipulating the way that data is set up to make it easier to interpret. For example, changing birth dates into age categories, or removing ‘don’t know’ categories.
- Weighting is a technique which adjusts the results of a survey to bring them in line with what is known about the population.
These steps are also sometimes referred to as data processing
It is possible to first clean the data, then tidy the data and, then, if necessary, weight the data. However, in practice it is much more efficient to simultaneously clean and tidy the data and then weight the data.
Basic process
Choosing Survey Analysis Software
The easiest option for analyzing survey data is usually to use the analysis tools that come for free in the Data Collection Software that has been used to collect the data. Where only rudimentary analysis is required, such as working out the proportion of people to select each option, this is usually the best approach. However, if there is a need to share reporting with others, to fix problems with the data or to conduct more sophisticated analyses, it is generally necessary to use software specifically designed for the analysis of survey data.
General-purpose software for analyzing surveys
Most people who analyze surveys do so using general-purpose survey analysis software. Some of the main programs for doing this are described in the table below. The next table provides an overview of more specialized types of software used in survey analysis.
The best way to evaluate whether the software is likely to be useful is via having a trial. This link takes you to tutorials which you can use to evaluate the different programs.
| Program | Typical user | Key features | Key limitations |
|---|---|---|---|
| Displayr[note 1] | Little or no experience in analyzing surveys | Ease of use and sharing resultsAdvanced analysis | Creation of complex crosstabs is less flexible than in WinCross, Survey Reporter and MarketSightDoes not support Tracking studies |
| MarketSight | Market research consultants and the internal research departments of large companies | Easy to learn/useQuickly create large numbers of crosstabs | No advanced analysis |
| Q[note 2] | Market research consultants and the internal research departments of large companies | Easier to learn and use than SPSSAdvanced analysis Weighting Automation (e.g., exporting to office, updating trackers) |
Creation of complex crosstabs is less flexible than in WinCross, Survey Reporter and MarketSight |
| Survey Reporter | Market research consultants and the internal research departments of large companies | Well-integrated with SPSS data collection products | No Advanced analysisAssumes you have access to a DP department that uses SPSS data collection products |
| WinCross | Market research consultants | Efficient and flexible creation of crosstabs | No advanced analysisRequires the user to do ‘programming’ |
| SPSS Statistics | Market research consultants, internal research departments, statisticians and ‘advanced quant’ teams | More than 10 times as many features as the programs listed above | Difficult-to-learn and generally less efficient to use than the other programs listed above |
| R | Statisticians and ‘advanced quant’ teams | AutomationCustomization More features than any of the other programs on this table |
Poor at creating crosstabsAlmost everything has to be done by ‘programming’ which makes it very slow to use relative to the other programs |
Overview of specialty survey analysis software
| Types of data analysis software | General-purpose survey analysis software | Data Processing Software | Variance Estimation Software | General-purpose statistical software | Data collection software that can can conduct basic analyses |
|---|---|---|---|---|---|
| Typical users | Consultants, marketers, market researchers | Data Processors (DP) people that create large numbers of crosstabs for their clients (where the clients are typically market research consultancies) | Statisticians | Statisticians and similar data analysis professionals | Students, industry associations, HR, small businesses conducting their own research |
| Examples | DisplayrMarketSight Q SPSS Custom Tables SPSS Survey Reporter Wincross |
MRDC Quantum SurveyCraft Uncle |
AM Software Bascula CENVAR CLUSTERS Epi Info IVEware Generalized Estimation System (GES) Rpackages: survey and pps SAS Stata SUDAAN VPLX WesVarPC |
SPSS StatisticsStatistica R Stata SAS |
Alchemer (formerly Survey Gizmo) Confirmit Insightify Polldaddy Obsurvey Qualtrics QuestionPro Snap Surveys Super Simple Survey SurveyMonkey Toluna QuickSurveys Wufoo Survey Crafter |
Getting a Data File
A data file contains the individual responses to a survey in a format that permits them to be analyzed by a program specifically designed for the analysis of survey data (e.g., SPSS, Q, Displayr, Stata). Almost all programs that are used to conduct surveys are able to export data files.
In much the same way that some meals are great while others are inedible, some data files are great and some are unusable. The quality of a data file is perhaps the biggest cause of problems experienced by people when learning how to analyze surveys, as a common mistake is to put insufficient effort into obtaining ‘good’ data which results in the analysis being much harder than it needs to be.
What survey data looks like
Raw data
When we conduct market research we usually (but not always) collect data about individual people, households or businesses.The data provided by respondents is called the raw data. The table below shows raw data for ten households (from a larger data file). Each row in a table of raw data represents the data from an individual respondent, and there are no blank rows. In this case, each respondent was a household. Each column is referred to as a variable. Each variable is a measure of some characteristic of the respondents.
| ID | CARRIER | INCOME | MOVES | AGE | EDUCATION | EMPLOYMENT | NON-USAGE | Q1a | Q1b | Q1c |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 1 | 1 | 3 | 2 | 1 | 9 | 1 | 1 | 1 |
| 2 | 1 | 4 | 3 | 2 | 2 | 1 | 2 | 1 | 1 | 1 |
| 3 | 2 | NA | 1 | NA | NA | NA | 6 | 1 | 1 | 1 |
| 4 | 2 | NA | 3 | 6 | 1 | 5 | 7 | 1 | 1 | 1 |
| 5 | 2 | NA | 1 | 6 | 2 | 4 | 0 | 1 | 1 | 1 |
| 6 | 2 | NA | 1 | 6 | NA | NA | 0 | 0 | 1 | 0 |
| 7 | 2 | 3 | 1 | 4 | 1 | 1 | 3 | 1 | 1 | 1 |
| 8 | 2 | 2 | 1 | 5 | 2 | 5 | 1 | 1 | 1 | 1 |
| 9 | 2 | NA | 1 | 5 | 1 | 1 | 0 | 1 | 1 | 1 |
| 10 | 2 | 3 | 1 | 4 | 1 | 4 | 2 | 1 | 1 | 0 |
Metadata
Data such as that above is not, on its own, readily interpretable. To interpret such data it is necessary to also have metadata, explaining what it all means. The metadata, which is sometimes referred to as a data dictionary, is shown below. So, returning to the table above, the database indicates that the fourth household was not a customer of AT&T, there is no data indicating the household’s income, the household moved twice in the last 10 years, the respondent who completed the survey was 65 or older, and so on.
Where a variable is categorical this means that the values stored in the raw data can only be interpreted by looking at the metadata. In particular, with the MOVES variable, a 1 indicates that a household has not moved, a 2 indicates it has moved once, etc. By contrast, with the USAGE variable, which is numeric, a 1 indicates it was used once, a 2 indicates it was used twice, etc.
| Variable | Variable Label | Value Labels | Variable Type |
|---|---|---|---|
| ID | A unique identification number assigned to each respondent | 1 = first respondent, 2 = second respondent,… | Categorical |
| CARRIER | Phone carrier of household | 1 = AT&T, 2 = Other | Categorical |
| INCOME | Household income bracket (in thousands) | 1 = <7.5, 2 = 7.5-15, 3 = 15-25, 4 = 25-35, 5 = 35-45, 6 = 45-75, 7 = >75 | Categorical |
| MOVES | Number of times the household has moved in the preceding 10 years | 1 = 0, 2 = 1,3 = 2, …, 8 = 7,11 = >10 | Categorical |
| AGE | Age of the respondent | 1 = 18-24,2 = 25-34, 3 = 35-44, 4 = 45-54, 5 = 55-64, 6 = 65+ | Categorical |
| EDUCATION | The highest level of education achieved | 1 = Did not finish school, 2 = High School; 3 = College, 4 = Postgraduate | Categorical |
| EMPLOYMENT | Employment status of the respondent | 1 = Full-time, 2 = Part-time; 3 = Student; 4 = At home; 5 = Retired; 6 = Unemployed | Categorical |
| USAGE | The typical monthly number of longdistance telephone calls by the household | Numeric | |
| Q1a | Aware: AT&T | 0 = No, 1 = Yes | Categorical |
| Q1b | Aware: Verizon | 0 = No, 1 = Yes | Categorical |
| Q1c | Aware: CenturyLink | 0 = No, 1 = Yes | Categorical |
This table shows the minimal metadata necessary to analyze a survey. However, better data files will contain more information. In particular:
- Question Type. For example, note that the last three variables, Q1a, Q1b and Q1c are related and form a part of a single question (which asked people which of the companies they had heard of); a good data file will contain metadata showing that these are linked together.
- Versioning. For example, changes to question wording that occurred during the data collection process and different translations.
A good data file will contain both the raw data and the metadata together in a single file. If you have two files, one which contains the raw data and another which contains the metadata, then you do not actually have a ‘data file’, you instead have the material you need to create a data file, but still have to create it. Many data analysis programs will provide tools that allow you to import the raw data and then enter the metadata but it will generally need to be done manually (i.e., by retyping it or cutting and pasting each field of information); this is a time consuming and error-prone process which should be avoided where possible.
Data files formats
Data collection programs export data files in a specific format. Most programs provide multiple formats for exporting, but these formats can differ markedly in terms of their usefulness.
Text files
The simplest data files are called ‘text data files’. It is generally a very bad idea to obtain the data from a survey as a text file. This is because when data is obtained as a text file there will be one of two problems:
- It will either contain no metadata, which makes it at best difficult to analyze and at worst impossible (e.g., if you do not know that a value of 2 represents an age of 25-34, then there is no way to interpret the data).
- It will contain text instead of numbers for all the data. Initially this may appear to be useful, but in practice is a massive problem, as:
- Most programs for the analysis of survey data do not permit you to do analysis with data in this format, and so you will read the data into the program and then discover that you either cannot do even the most basic analysis, or, need to spend a lot of time re-formatting the data to make it useful.
- Many of the important features of the survey will not be evident in the data file. For example, if you have asked a question getting people to give ratings from 0 to 10, when you create a table in a text file they will be ordered as: 0, 1, 10, 2, 3, …. Similarly, Grid and Multiple Response questions will generally need to be treated as if they were multiple Single Response questions.
| ID | CARRIER | INCOME | MOVES | AGE | EDUCATION | EMPLOYMENT | USAGE | Q1a | Q1b | Q1c |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Other | <7.5 | 0 | 35-44 | High School | Full-time | 9 | Yes | Yes | Yes |
| 2 | AT&T | 45-75 | 2 | 25-34 | High School | Full-time | 2 | Yes | Yes | Yes |
| 3 | Other | NA | 0 | NA | NA | NA | 6 | Yes | Yes | Yes |
| 4 | Other | NA | 2 | 65+ | Did not finish school | Retired | 7 | Yes | Yes | Yes |
| 5 | Other | NA | 0 | 65+ | High School | At Home | 0 | Yes | Yes | Yes |
| 6 | Other | NA | 0 | 65+ | NA | NA | 0 | No | Yes | No |
| 7 | Other | 25-35 | 0 | 45-54 | Did not finish school | Full-time | 3 | Yes | Yes | Yes |
| 8 | Other | 15-25 | 0 | 55-64 | High School | Retired | 1 | Yes | Yes | Yes |
| 9 | Other | NA | 0 | 55-64 | Did not finish school | Full-time | 0 | Yes | Yes | Yes |
| 10 | Other | 25-35 | 0 | 45-54 | Did not finish school | At Home | 2 | Yes | Yes | No |
CSV Files and Excel files
This is generally the best of the text file formats (although this is very much a case of being the tallest dwarf). It uses a comma to separate each variable.
Tab delimited files
This is similar to a CSV file, except that a tab character is used instead of a comma. Generally, if data is in this format it is appropriate to open it in Excel and then save it as a CSV file.
Fixed width files (ASCII) files
A fixed width file is one where each column of numbers has a specific meaning. For example, in the data below the first column may represent the first variable, the second and third columns together may represent the second variable, and so on. This format was invented because it took up little hard-disk space, which was an important consideration in the 1960s and 1970s. It is rarely used today and is the worst of all of the file formats as it cannot readily be used with Open-Ended questions and most modern programs will not read this file format. Generally, if data is in this format it is appropriate to open it in Excel and then save it as a CSV file.
00001 01200 01203
Good data files
The good formats
The gold standard data file is an IBM SPSS Data Collection Model data file (also known as a Dimensions, MDT or MDD data file). This file format contains all the different types of metadata. This data file is only created by the top-of-the-range IBM data collection programs and can only be read by IBM data products and a small number of other products (Q and Displayr).
The next-best format is the Triple S format. It is a little more widely used than the IBM SPSS Data Collection Model format, but it is generally only available in the more expensive data collection programs.
The industry standard ‘good’ file format for data is an SPSS .SAV data file (usually called a ‘dot sav’ file). This is not quite as good as the other two formats, as it does not contain the versioning information and it only contains very limited Question Type information (it does not support the various Grid type of questions). However, all good data collection programs can export in this format. Refer to SPSS Data File Specifications for details on how these files are best set up.
Occasionally data collection programs will export both a text file and an SPSS .sps file (also known as a syntax file). The syntax file is actually a program which contains instructions for turning the text file into an SPSS .SAV file. SPSS is the the only program that can always read these files, but Q can read these in some circumstances.
Appropriate set up in the good formats
Obtaining a good data file is not just a case of specifying the desired format. In particular, in the case of the SPSS .SAV data files, it is quite common to have them created with either incorrect values and incorrect metadata. The most common problems are:
- Incorrect values for options not selected in multiple response questions. That is, the files use the same value (commonly a 0 or a special character/value indicates missing value category usually called SYSMS, NA, or NaN) to indicate that somebody was not asked a question as they use to indicate that somebody did not select an option in a Multiple Response question.
- Labels that have been truncated (e.g., saying Please rate your satisfaction with the following ba), making it impossible to determine what the data means (except by reviewing the questionnaire).
Most survey analysis programs will have some facilities in them to clean such poor data, but it is generally advisable to try and instead obtain a data file that does not contain such problems.
What a Data File Looks Like
Useless: Typical Tables of Survey Results
The term ‘data file’ is a bit misleading, as files are only useful if they contain data in the appropriate format. For example, the data shown below is largely useless. Yes, it shows some results from the survey. However, it is impossible to use this data to compute many useful things. For example, this data cannot be used to work out if males were more likely to be satisfied than females.
Useful: Tables Containing One Row Per Respondent
By contrast, the data below is appropriate for data analysis. This table contains:
- A column for each of the different bits of data collected in the survey (e.g., age is in one column, education is in another).
- A single row at the top containing the headings that describe each column.
- A separate row for each respondent (i.e., all the data for the first respondent is shown the row under the headings, the row beneath this contains the data for the second respondent, and so on).
Correcting Metadata
The metadata of a data file is often incorrect and the first step in analyzing data is often to correct these errors. Where there are a substantial amount of errors in metadata it is often the case that the best solution is to try and get a better data file. This page lists the most common problems and their remedies.
Combining variables into multiple response questions
A very common problem with data files is that a question that was asked as a multiple response question appears as multiple single response questions. This is generally caused by the data collection software exporting the data incorrectly (unfortunately, most data collection programs make this mistake). Some programs, such as Q and Displayr, attempt to automatically correct this problem by looking for patterns in the data (e.g., if there are 10 variables, each of which has the same prefix of Awareness with and have the same code frame, then Q and Displayr automatically group the variables together). However, in most programs there is a need to manually group together variables as multiple response questions.
There are two common variants of this problem.
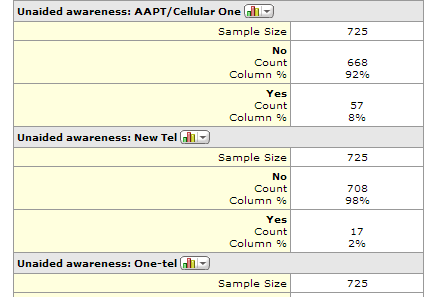
Multiple binary variables
Each category of the question appears as a separate summary table, with two categories (hence the term ‘binary’). For example, the following shows a part of a MarketSight Summary Report, which reveals that a question titled Unaided Awareness has been shown as multiple separate tables, rather than being grouped together. This problem has a number of different causes. One of them is that often the data file does not contain the relevant metadata. The other is that sometimes the information is in the file but the data analysis program does not interpret it properly (in this example, both Q and Displayr do group these variables together as a multiple response question).
All the major analysis programs have in-built tools designed to combine multiple variables together and thereby solve this problem.
See How to Combine Variables into Multiple Response Questions and Grids.
Multiple categorical variables
There are multiple tables (or variables) showing all of the different categories. Typically, the first table shows the first response that a respondent selected, the second shows the second response and so on.
All the major analysis programs have in-built tools designed to combine multiple variables together and thereby solve this problem.
Combining variables into grids
In just the way that multiple response questions are sometimes not correctly represented in a data file, requiring the variables to be combined (see the previous problems), often grid questions will also initially appear split apart. Furthermore, many data analysis programs (e.g., SPSS, MarketSight and R) do not provide support for many types of grids.
Splitting questions
In some situations, variables are represented as grids or multiple response questions when it is more appropriate to instead represent them as separate variables. In particular, Q and Displayr automatically group together variables when they import data. From time-to-time, they are over zealous and group together variables that should not be grouped together, requiring that they need to be split apart.
See How to Split Questions Into Separate Variables.
Changing variable type
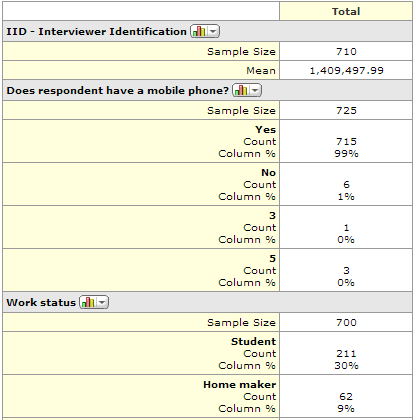
Most of the more modern survey analysis programs (e.g., R, Q, Displayr and MarketSight) use metadata to automate how they produce summary tables. For example, in the following output from MarketSight, the average is shown for IID - Interviewer Identification whereas percentages are shown for the other variables. This is because the metadata indicates that IID - Interviewer Identification is a numeric variable while Does respondent have a mobile phone? is a categorical variable. Thus, when the the metadata show the wrong Variable Type, this causes the output to be inappropriate. The remedy is to change the variable type.
See How to Change Variable Type and Question Type.
Changing question type
In addition to allowing the user to change from numeric to categorical and back, Q and Displayr also allow the user to change between different question types. Consider the table from Displayr below on the left. The metadata in this example has treated this table as a multiple response question, but the table on the right is automatically generated instead when the metadata is changed to indicate that the question is, in fact, a grid.
Question wording
Commonly data files will either refer to questions by their question number (for example, a question showing age data may be referred to as #q43, or some of the wording is shown but it is either messy or truncated (e.g., Please rate your satisf). In most programs it is a straightforward process for modifying these names.
See How to Change the Name of a Question or Variable.
Category wording
The following table, from SPSS, shows a quite common problem, where numbers appear instead of descriptions for some of the categories in the table. The key challenge that this usually presents is working out what the numbers really mean; there is usually no way of working this out directly from the data (i.e., you need to ask whoever created the data file). Once this is known it is usually quite straightforward to fix the problem.
Missing Values
One of the trickiest aspects of cleaning and tidying a data file relates to missing values, which are also known as missing data. A value is said to be ‘missing’ where there is no valid data for a particular respondents for a variable. How missing values are treated when cleaning a data file can have a large impact on any conclusions from the analysis.
How programs treat missing values (re-basing)
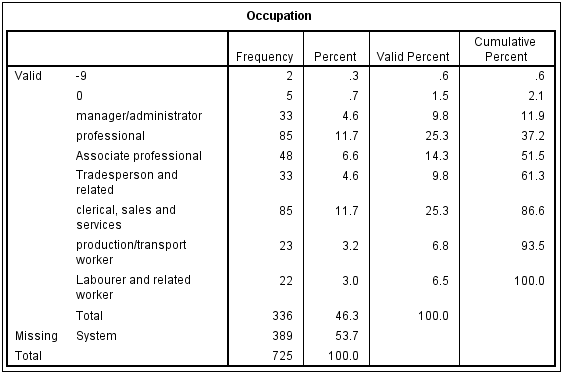
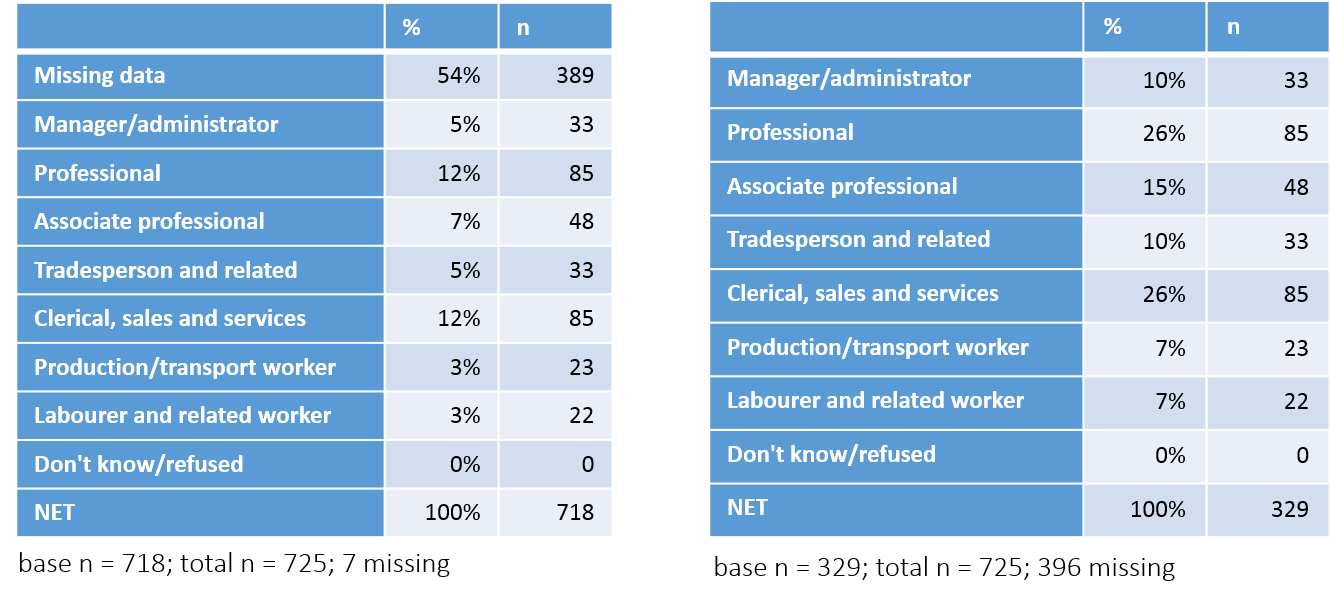
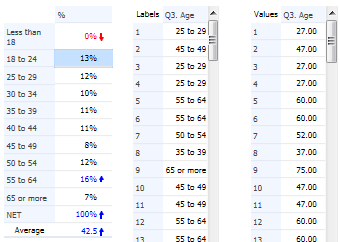
The tables below have been created by exporting to PowerPoint from Q. Looking first at the table on the left, note that in the bottom row it reports that the NET (which in this case is a total) is 100% and that this corresponds to 718 respondents (n). Each of the percentages on this table has been computed by dividing the number of people to select each option (n) by the total sample size. For example, the 5% for Manager/administrator is computed as 33 / 718. The first row on this table shows that 54% (389) of the respondents have missing data, which in this case was because they were students, retired, unemployed or home-makers.
The table on the right, by contrast, has excluded the respondents with missing data. Consequently, its total sample size, as shown in the bottom row of the table and also the base n in the footer of the table, is 329 (i.e., 718 – 389). Note that in this table all the percentages are different. For example, the 33 Manager/administrators in the sample now correspondents to 10% of the sample.
The table on the right has been re-based; that is, the percentages have been computed with the missing data excluded from the calculations. This is done automatically by most survey analysis programs. However, to do this automatically the programs need to know which categories to treat as being missing. In the case of the table on the left, although the first category has a label which says it is missing data, there is not metadata which explicitly tells the program it is missing data. Consequently, it appears on the table and is analyzed in the same way as all the other categories. By contrast, with the example on the right, the program has been told to treat the people with missing data as being actually missing and the percentages are updated accordingly.
It is important to appreciate that neither of the tables is necessarily wrong. Rather, they just have different interpretations. The table on the left shows that 5% of people are Managers/administrators, whereas the table on the right is interpreted as saying that 10% of employed people are Managers/administrators.
See How To Remove a Category and Re-Base a Table for information on how to re-base tables in different programs.
Common missing data situations
As the previous example illustrated, whether or not data should be treated as being missing is a decision that has to be made by the person analyzing the data, as the way that it needs to be treated depends upon context (e.g., in the case above, whether we wanted to compute proportions in the total sample or just among people that were employed).
Often the data will be automatically marked as being missing. In particular, with good quality data files any respondent who has not been asked a question will automatically be classified as having missing data on that question and any analyses will be automatically re-based with that respondent’s data removed. Consequently, the main situations where the missing data metadata needs to be modified are:
- Where respondents have data that is marked as missing but who should not be treated as having missing data. Consider variables showing the number of children that people have in different age bands (e.g., the number of children aged under 2, from 2 to 5, etc.) Typically, where a person indicates they have no children they end up not being asked how many children they have in each age group and thus end up having missing values in the data file for the number of children in age group. However, in this instance we actually know that they have 0 children in each age category so the data needs to be changed from missing values to instead show that the data is not missing (see Recoding Variables).
- Where respondents have data that is not marked as missing but should be marked as missing. For example, in a study of voting intentions if 10% of the sample have said “Don’t know” it often makes sense to treat these responses as missing data – otherwise the polling results indicate that that preference shares for the different political parties add up to less than 100%.
Merging Categories and Creating NETs
Some programs, such as Q and Displayr, allow you to modify the data so that whenever you create tables the merging and netting of categories is remembered. Other programs, such as SPSS Custom Tables, Survey Reporter and MarketSight, work by letting you create new combined categories at the time of creating crosstabs, while others require you to instead create new categories as new variables by recoding existing variables (e.g., SPSS, R).
Recoding Variables
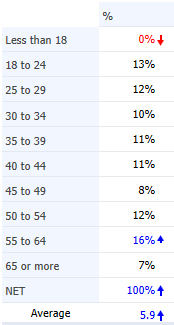
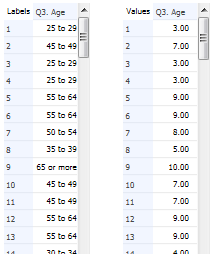
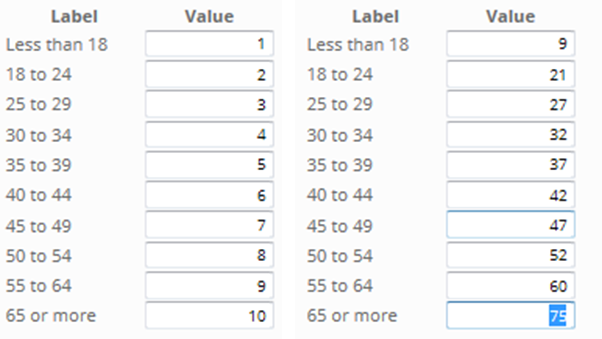
The reason for this curious average age calculation is that categorical variables, such as age, are usually stored in the data file with a 1 for the first category, a 2 for the second category and so on. This is shown below, where on the left we can see the age categories for 13 respondents while on the right we can see the values that are stored in the data file. When the average was computed it was computed using these values (e.g., somebody aged 25 to 29 was given a value of 3 when computing an average).
The left example below shows the original values in the data file. The values on the right show the values after recoding. This is an example of mid-point recoding, where the value assigned is the value in the middle of the range (e.g., 27 is in the middle of 25 to 29).
The recoded numeric variable is shown on the right below, and we can see from the table on the left that the average is now a much more sensible 42.5.
Coding Text Variables
Coding refers to the process of creating a categorical variable.
Text data
The following table shows the first ten responses to an open-ended question asking people why, in their opinion, people preferred different brands of colas.
| People who drink Pepsi Max probably prefer sugar – free drinks |
| Big or large people drink Pepsi light and normal size people drink Pepsi Max |
| I prefer the flavour of Diet Coke to Pepsi and that is what I base my decision on |
| ??????????????? |
| Probably the diet or light colas appeal to those who want to reduce their sugar intake, which traditionally I suppose, is women. I found that once I stared to drink the light colas, I really disliked the taste of the other ‘full strength’ ones. If Coke or Pepsi are on special, I will buy the cheaper, because after the first drink, I adjust to the differences between the brands, and I like both. |
| Pepsi is full of sugar and Im a diabetic…. |
| Pepsi gives the impression of being a “home brand” type drink and coke zero is used by people who want to impress |
| traditionalists versus rebels |
| health conscious |
| People who drink Coke Zero are health concious |
Developing a code frame
Reading through the text data we can identify some themes. For example, we can classify the responses as falling into one or more of the following responses. Such a list of categories created from text data is known as a code frame. The number of each category is typically called the code when doing coding but it is the same as the value of a variable.
| Value | Label |
|---|---|
| 1 | Sugar-free |
| 2 | Taste |
| 3 | Weight/Health |
| 4 | Price |
| 5 | Image |
| 6 | Other |
The creation of a code frame is a highly subjective process. There’s a good chance that if you read through the list of text data above you would have come up with a different code frame. For example, in the above code frame Sugar-free is distinct from Weight/Health, but an argument can be made that they are the same, with Sugar-free being a feature that ladders to Weight/Health. One approach to resolving this is to get a few different people to independently code the data and then resolve discrepancies by discussion, but such a rigorous approach is extremely rare outside of small academic studies.
Coding
The final stage of coding, which is itself called coding, involves assigning each response to one or more codes (one if it is to be interpreted as a single response question and more if it is interpreted as a multiple response question). Again, as with creation of the code frame this is a subjective process and greater accuracy can be obtained by getting multiple people to code the same data (but, such rigor is extremely rare in commercial studies).
| People who drink Pepsi Max probably prefer sugar – free drinks | 1 |
| Big or large people drink Pepsi light and normal size people drink Pepsi Max | 3 |
| I prefer the flavour of Diet Coke to Pepsi and that is what I base my decision on | 2 |
| ??????????????? | Missing Value |
| Probably the diet or light colas appeal to those who want to reduce their sugar intake, which traditionally I suppose, is women. I found that once I stared to drink the light colas, I really disliked the taste of the other ‘full strength’ ones. If Coke or Pepsi are on special, I will buy the cheaper, because after the first drink, I adjust to the differences between the brands, and I like both. | 1, 2, 4 |
| Pepsi is full of sugar and Im a diabetic…. | 3 |
| Pepsi gives the impression of being a “home brand” type drink and coke zero is used by people who want to impress | 5 |
| traditionalists versus rebels | 5 |
| health conscious | 3 |
| People who drink Coke Zero are health consitious | 3 |
Creating New Variables
Often it is useful to construct a new variable. Sometimes, this will be a numeric variable. For example, if one question asks about the number of bottles of Coke consumed in a week and another asks about the number of bottles of Pepsi it may be useful to work out the number of bottles of cola consumed. Other times it will be useful to create a categorical variable. For example, it may be useful to combine together questions about age, marital status and children to create a new categorical variable indicating family life stage (e.g., young singles, young couples, etc.).
Copying, merging and recoding
Often a new variable needs to be derived from an existing variable. For example, it may be that there is an existing variable with categories of Strongly Disagree, Somewhat Disagree, Neither Agree nor Disagree, Somewhat Agree and Strongly Agree, and there is a desire to create a new variable with categories of Agree and Not Agree. In such a situation the straightforward approach is to copy the existing variable and then merge the categories in the copied variable. Where programs do not permit the user to merge categories, such as in SPSS, the same outcome can be achieved by recoding.
Automatic categorization
The more sophisticated programs, such as SPSS, R and Q have various in-built tools for automatically categorizing numeric variables (e.g., into quartiles).
Formulas
The most powerful, but also most complex, way of creating new variables is to use formulas. For example, if wanting to create a new numeric variable by adding two variables called q1 and q2 most programs will have a facility to create a new variable using a formula such as:
q1 + q2
Or, if creating a new categorical variable the formula may look something like:
if (age <= 35){
if (numberChildren == 0) {
if (married) 2; //young couples
else 1; //young singles
}
else {
if (married) 3; //young families
else 4;// young single families
}
else{
if (numberChildren == 0) {
if (married) 2; //older couples
else 1; //older singles
}
else {
if (married) 3; //older families
else 4;// older single families
}
}
Multivariate analysis
Many multivariate analysis methods, such as Factor Analysis and Latent Class Analysis automatically output new variables that are summaries of the data.
Deleting Respondents
- Creating a new filter variable that indicates who needs to be deleted (or, who should not be deleted).
- Giving the analysis program an instruction to delete the respondents’ data.
Checking Representativeness
Checking the representativeness of a study involves trying to work out if the data from the study is consistent with what is known about the population that the study seeks to understand.
Basic process for checking representativeness
- Collect secondary data on your population (e.g., age, gender, place-of-residence, brands purchased).
- Ensure that the questionnaire is written so that the survey data can be easily compared with the secondary data.
- Compare the secondary data with the results of the survey.
- Choose to either:
- Weight the data.
- Discard the data.
- Use the data as it is.
Example
The table below shows the proportion of people in different age bands in a survey of the phone market. A quick examination of the data reveals that something is wrong. For example, only 3% of the sample are aged 30 to 34, whereas approximately 10 times this number are aged 20 to 24. This suggests that the sample may not be representative of the population at large.
| Age | Survey |
|---|---|
| 15 and under | 0.1% |
| 16-19 yrs | 10.2% |
| 20-24 yrs | 32.0% |
| 25-29 yrs | 14.8% |
| 30-34 yrs | 3.5% |
| 35-44 yrs | 4.9% |
| 45-54 yrs | 27.7% |
| 55-64 yrs | 5.0% |
| 65 and over | 1.8% |
| Total | 100% |
In order to be confident that a sample is or is not consistent with what is known about a population we need some other data about the population. Ideally this will be from a source with known reliability, such as sales statistics or government studies of the market. However, it can also be obtained from other surveys where there was a good reason to believe in their representativeness. As an example, the following data shows the required age in the population for the survey.
| Age | Population # | Population % |
|---|---|---|
| 15 and under | 10,670,000 | 3.3% |
| 16-19 yrs | 20,914,000 | 6.5% |
| 20-24 yrs | 25,619,000 | 8.0% |
| 25-29 yrs | 25,107,000 | 7.8% |
| 30-34 yrs | 24,605,000 | 7.7% |
| 35-44 yrs | 48,225,000 | 15.0% |
| 45-54 yrs | 47,261,000 | 14.7% |
| 55-64 yrs | 46,316,000 | 14.4% |
| 65 and over | 72,623,000 | 22.6% |
| Total | 321,340,000 | 100% |
Putting the sample results side-by-side with the known data for the market quickly reveals the scale of the problem with this particular study. Looking at the first row of numbers in the table below we can see that 0.1% of the sample were aged 15 and under, which compares to 3.3% in the population and thus the true proportion in the population is approximately 23.8 times that observed in the study (as all the numbers are rounded you will get a slightly different answer if you attempt to reproduce this calculation). Reading down the right-most column of the table we can see that there are no instances where the ratio of the percentages is at 1.0, which is approximately what is required for the study to be representative (small deviations are acceptable due to sampling error).
| Age | Survey (A) | Population # | Population % (B) | (B)/(A) |
|---|---|---|---|---|
| 15 and under | 0.1% | 10,670,000 | 3.3% | 23.8 |
| 16-19 yrs | 10.2% | 20,914,000 | 6.5% | 0.6 |
| 20-24 yrs | 32.0% | 25,619,000 | 8.0% | 0.2 |
| 25-29 yrs | 14.8% | 25,107,000 | 7.8% | 0.5 |
| 30-34 yrs | 3.5% | 24,605,000 | 7.7% | 2.2 |
| 35-44 yrs | 4.9% | 48,225,000 | 15.0% | 3.1 |
| 45-54 yrs | 27.7% | 47,261,000 | 14.7% | 0.5 |
| 55-64 yrs | 5.0% | 46,316,000 | 14.4% | 2.9 |
| 65 and over | 1.8% | 72,623,000 | 22.6% | 12.4 |
| Total | 100% | 321,340,000 | 100% | 1.0 |
A similar process would then need to be performed for any other secondary data. Then, once all the comparisons have been done, a decision needs to be made, where the options are:
- Conclude that the data from the sample is consistent with what is known about the population. In this example such a conclusion is clearly not warranted.
- Weight the data, which involves adjusting how the data is analyzed so as to take into account the nature of differences between the sample and the population. This option only makes sense if any deviations between the survey’s results and the population are considered to be ‘sensible’. Typically, results as disparate as those shown above would indicate that the study was fundamentally flawed. However, there are scenarios when such discrepancies may be considered plausible. For example, it is commonly the case that women are more likely to respond to surveys than men and so if a survey exhibited an over-representation of women and all the discrepancies between the survey and secondary data could be explained by such a phenomena, then weighting would be a sensible remedy.
- Discard the data. That is, conclude that the discrepancies are so great as to render the survey untrustworthy. The discrepancies shown in the example above would suggest that such a conclusion would be justified, as if the survey is so inaccurate in terms of reflecting the population’s age then it is reasonable to assume it will be similarly inaccurate for other questions in the survey where there is no way of checking. In practice, it is extremely rare to ever discard a survey, as most people take the view that it is better to have a bad survey than no survey.
Weighting
Weighting is used to adjust the results of a study to bring them more in line with what is known about a population. For example, if a sample contains 40% males and the population contains 49% males, weighting can be used to correct the data to correct for this discrepancy.
Worked example
Consider the following data showing 10 people’s favorite celebrity:
Brad Pitt Brad Pitt Brad Pitt Brad Pitt Brad Pitt Brad Pitt Brad Pitt Brad Pitt Tiger Woods Tiger Woods
In this sample of ten, 80% of people have nominated Brad Pitt as their favorite celebrity. When we conduct market research studies, the whole point is to draw conclusions about the population, rather than just our sample, so we should go one step further and, rather than say “80% of the sample nominate Brad Pitt as their favorite celebrity” we should instead be conducting research so that we can say “Brad Pitt is the most popular celebrity, with 80% of people nominating as their favorite (we should also communicate the precision, as discussed in Determining The Sample Size.
Now, consider the impact of some additional information about the gender of our ten respondents:
Brad Pitt Female Brad Pitt Female Brad Pitt Female Brad Pitt Female Brad Pitt Female Brad Pitt Female Brad Pitt Female Brad Pitt Female Tiger Woods Male Tiger Woods Male
From this data we can see that the sample is unrepresentative in terms of gender, with eight of ten respondents being female 80%) and two being male (20%), compared to the true representation in the world of about 50% men and 50% women. Furthermore, gender seems to be the sole determinant of preference. As the sample is not representative in terms of gender and gender is correlated with our measure of favorite celebrity, it follows that any estimate of the favorite celebrity will only be valid if we take into account the over-representation of women in the sample.
We can improve our estimate by weighting. A weight is computed for every respondent in a sample, and it is computed by dividing the correct proportion by the observed proportion. The correct proportion of males in our population is 50% and the observed proportion is 20%, so the weight for each male is 50%/20%=2.5 and the weight for each female is 50%/80%=0.625. Thus, our data becomes:
Favourite Celebrity Weight Brad Pitt 0.625 Brad Pitt 0.625 Brad Pitt 0.625 Brad Pitt 0.625 Brad Pitt 0.625 Brad Pitt 0.625 Brad Pitt 0.625 Brad Pitt 0.625 Tiger Woods 2.5 Tiger Woods 2.5
We now compute our estimate of the proportion of people to have Brad Pitt as their favorite celebrity by summing up the weights of each of the respondents to prefer Brad Pitt and dividing this by the sum of all of the respondents’ weights:
The approach described here for computing a weight is a relatively simple case, but the basic idea can be extended to deal with much more complicated cases (e.g., it is routine to simultaneously weight by geography, gender and age).
Weighting using standard analysis software
With the exception of Q, none of the general-purpose survey analysis programs contain useful tools for creating weights. Consequently, weights are usually created by either:
- Have them computed using data processing software. Most companies that collect data offer the creation of weights as a service and it is commonplace to have weights included in the data file.
- Compute them manually. That is, you need to:
- Compute the observed proportion of people that have selected each answer.
- Obtain the targets (i.e., the results believed to apply in the population; in the example above the targets were that 50% of the population was male and 50% was female.
- Compute the weights by dividing targets by the observed proportions (note that this is only one approach to weighting and more complicated approaches to weighting, such as rim weighting cannot be done this way.
When weighting does and does not work
Consider the situation where a survey was well managed but due to some anticipated quirk of how the data was collected it over-represent males. If gender is known to relate to other variables of interest in the survey then it follows both that:
- The data needs to be weighted or otherwise any analyses will be misleading (as they will be biased by the misrepresentation of gender).
- The weighting will fix the data.
However, what if the gender problem is one of many unknown problems in the data? Imagine that the survey is also biased towards low income people, towards people that like to do surveys and towards people that do not get out of doors much. Fixing the gender problem by weighting will not fix any of these other problems. Furthermore, in general we will not know that we have these other problems, as we will have no data to check for representativeness.
The distinction between these two cases is crucial. Where the data is observed to be unrepresentative, weighting will only fix the data if there is good reason to believe that this is the only way in which the data will be representative.
Multiple Response Data Formats
Binary
Each category of the multiple response question is represented as a separate variable. Typically a 1 is used when an item has been selected and a 0 otherwise.
Max-Multi
Each variable can contain multiple categories, one for each of the options in the questionnaire. For example, if the question has 20 brands, but nobody selected more than five brands, it is possible to store the data as five variables, with the first containing one of the responses, the second another, and so on. There is no widely used term for this way of storing multiple response data; it is sometimes referred to as max-multi data.
Pros and cons of the different formats
The binary format is the standard and, in most situations, the preferable format. This is because it:
- Makes data analysis easier (as it is easier to compute new variables).
- Makes it possible to have missing values. For example, in a tracking study if a brand is in the questionnaire in some waves but not other waves then this can be reflected using a missing value in waves when it is not available. By contrast, where max-multi coding is used it is impossible to determine from the data whether an option was not selected, or, was not available.
The max-multi format’s advantages are:
- It uses up less memory on the computer (i.e., because it takes less variables). In the 1970s this meant that the max-multi was the standard format. Now, however, it tends to only be used sensibly in situations where there are questions with extremely large code frames (e.g., a list of 6,000 brands of car).
- It is easier to create if manually entering data (i.e., it is much easier for a data entry person to type 2, 5 to indicate that the second and fifth categories were selected than it is for them to enter lots of 1s and 0s).